压电测试仪之多层压电陶瓷变压器的振动与疲劳
推荐使用:GDPT-900A型变温压电测试系统，ZJ-3型静压电测试系统
压电变压器早于1956年由C．A．Rosen提出。20世纪80年代初，清华大学提出了多层独石化压电变压器的创意及概念，并在国际上早开展了多层压电变压器的研究。由于压电变压器升压比高、电磁干扰小、转换效率高、体积小、质量轻、输出波形好等优点，近年来在液晶显示器背光电源、高压臭氧发生器、空气清新器、雷达等领域中获得了应用。
压电变压器是电场与振动场间相互耦合的谐振器件，在谐振状态下，器件会因负载、使用环境、输入电压、材料等因素，产生发热、疲劳甚至断裂等问题。有关压电陶瓷材料疲劳的研究较多，学者提出了一些疲劳机理，目前广为大家接受的解释主要有畴夹持模型、电极连接不合适以及内应力集中。Zuo等人认为，在电场的作用下，由热应力引起的微裂纹将成为裂纹扩展的根源。Ru等人的研究表明，多层陶瓷器件失效的主要机制是电极与陶瓷材料之间的界面开裂以及电极端部的界面开裂。Gong等人通过非线性有限元法模拟了多层压电器件中内电极周围的电场分布，并发现在内电极端部边缘的电场分布非常不均匀，因此电极周围的陶瓷材料因铁电转变或电致伸缩而产生不协调变形，形成裂纹。为下一步深入研究压电变压器微裂纹的形成及扩散机理，本实验研究了压电变压器的微振动及疲劳行为。采用激光扫描测振仪以及 疲劳加载实验测试压电变压器的特性变化。
1 压电变压器机理及结构
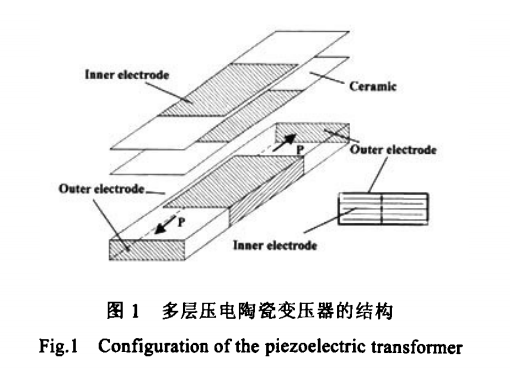
通过掺杂CdCO、SrCO?、ZnO或Li2CO?获得压电变压器所用高性能低烧兼优的Pb(Mg?/?Nb?/?)O?．Pb(Ni?/?Nb?/?)O?一Pb(ZrTi)O?压电材料。多层压电变压器的结构如图1所示。器件内部有19层陶瓷介质，外形尺寸约30 mm8 mmx3 mm。输入电极在器件的中部，输出电极分布在器件的两端。在交变输入电压以及机电耦合系数k??和k??的作用下，变压器沿长度方向发生谐振。对于半波谐振，有一条节线出现在器件的中心位置，对称的振动使变压器在两端产生相同的输出电压，即升压比相同。
利用有限元分析软件，对多层压电变压器的振动模态进行了理论计算与分析。分析采用的特性参数见表1。有限元法获得变压器半波谐振频率约55 kHz，全
波谐振频率约110 kHz。 
2 谐振频率的测试
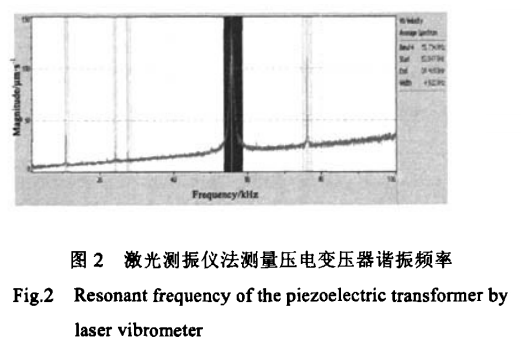
测定多层压电变压器的谐振频率主要包括两个方法：用Polytec OFV 056测振扫描探头对样品在一定频率范围扫描，获得样品在激光入射方向上样品表面各点的振动速度与位移；用信号发生器与示波器配合，观测输出电压，终测得谐振频率。 选择扫频模式(FFT)钡IJ试样品表面的振动，得到振动速率对频率的曲线，如图2所示。样品在55．7 kHz出现了明显的峰值，表明样品在该频率发生谐振，结合有限元分析结果，可以确定在55．7 kHz频率处于半波谐振模态。
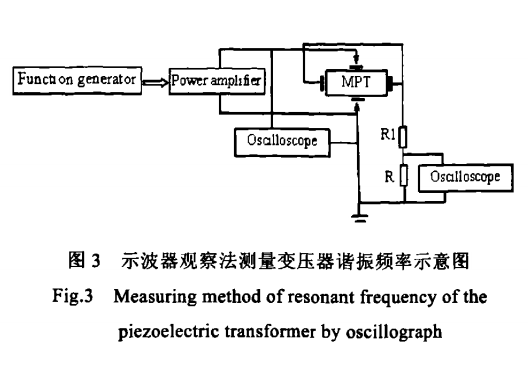
根据谐振原理，当压电变压器处于谐振时，其振动为强烈，升压比达到局部极大值。因此，控制输入信号的波形和电压幅值不变，改变输入信号的频率，通过观察输出电压幅值的变化，可以更地测定样品的谐振频率。实验装置见图3。其中，信号发生器为DF1692型多功能任意波形发生器，变压器专用功率放大器为KH-1A型宽带功率放大器，示波器为TDS5054数字荧光显示示波器，R1代表94 kΩ的水泥电阻负载，R代表4 kΩ的串联小电阻。
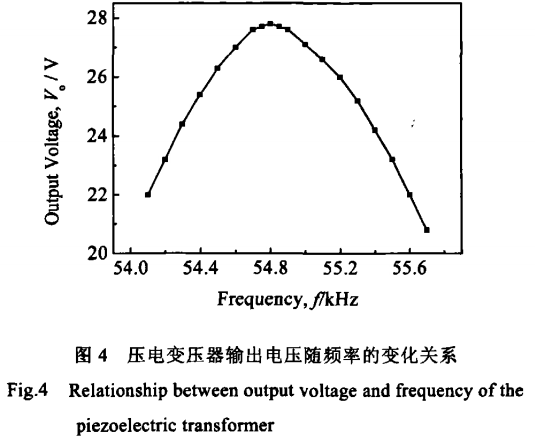
信号发生器输出正弦波形，实际输入电压峰峰值约10 V。在粗测谐振频率55 kHz附近微调频率，测量串联小电阻两端的输出电压，如图4。输出电压的极大值出现在54．8 kHz处，此为样品的实际谐振频率。
3 疲劳加载实验
疲劳加载实验条件：输入信号的波形为正弦波，频率为半波谐振频率54．8 kHz，电压峰峰值为30 V(实际工作电压在12 V以下)。输出负载为94 kΩ无感电阻。设置循环加载次数为109次，即连续振动约5 h。
3.1 谐振频率的漂移
由于疲劳加载可能会导致谐振频率的改变，因此在各项对比分析之前，首先需要重新测定变压器样品的半波谐振频率。用示波器观察疲劳加载后变压器样品的输出电压，确定疲劳后谐振频率为55．6 kHz，与疲劳加载前的谐振频率54．8 kHz比，相对漂移量约1.5％。
3.2 谐振模态振动的衰退
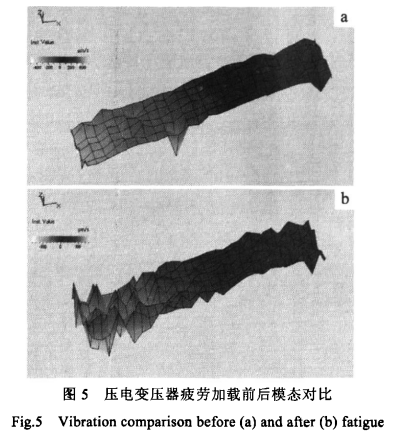
使用激光测振仪，在定频模式测得疲劳加载后变压器样品在一个振动周期里的图像。图5a中，各测量点的振动相位比较一致，说明在疲劳加载前，变压器样品长度方向上的形变十分协调：图5b中，各测量点的振动有些杂乱，这说明在疲劳加载后样品振动有些不稳定。从直观上可以判断，疲劳加载使得变压器样品的振动表现有所衰退。定量分析上，图5a中显示输出端端部的振动速率在300μm／s左右，而图5b中仅在100 μm／s左右。由此表明，疲劳加载除了使多层压电 变压器的形变与振动的协调性变差外，还使得整体的振动速率下降，振动幅度变小。
输入信号的频率固定在样品的半波谐振频率54.8kHz处，改变输入信号的电压幅值，测得输入端端部振幅Ai对输入信号电压峰峰值VP-P的曲线，如图6所示。在输入电压小于4 V时，变压器输入端振幅与输入电压呈现线性关系；当电压大于4V后，进入非线性区；大于10 V后，振幅逐渐趋于饱和。
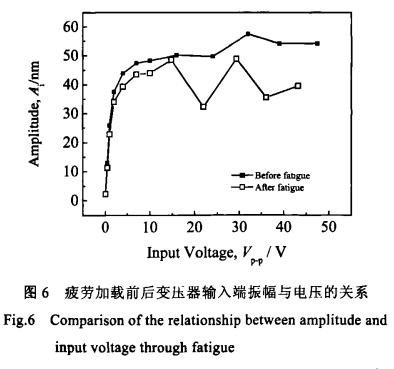同时，疲劳后的输入端振幅平均比疲劳前减少超过10％，且疲劳后的曲线不稳定。这说明109次的循环加载引起了变压器样品的部分疲劳，样品的端部及整体的振动幅度和速率都减小了约10％。但输入电压小于4 V时，输入端振幅与输入电压的线性关系较好。 3.3 疲劳加载前后输入输出特性的对比 由于负载对输入输出特性的显著影响，测试需要在不同的负载电阻下重复数次，结果见图7。当输入电压峰峰值小于20 V时，在4个负载阻值下，输出电压与输入电压都保持了较好的线性关系。当负载的阻值小于110 kΩ时，在10 v至U60 V的整个电压峰峰值的范围内，输出电压都随输入电压的增加而线性增加；当负载电阻大于160kΩ时，输出电压在输入电压峰峰值大于20 v起逐渐显示出非线性。
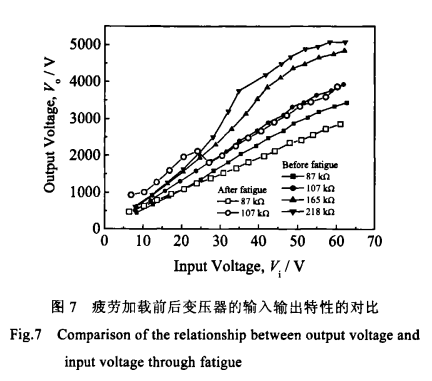根据图7中负载电阻87 kΩ对应的两条曲线，可知疲劳加载后的曲线绝大部分低于疲劳加载前的，即在10～60 V的输入电压峰峰值范围内，疲劳加载后变压器样品的升压比总体来看是降低了，约是疲劳前的85％左右，这与输入端端面振动幅度的减小比率也比较符合。 4结 论
1)有限元法获得变压器半波谐振频率约55 kHz，全波谐振频率约110 kHz。
2)激光测振仪测得压电变压器半波谐振频率为55．7kHz；信号发生器与示波器配合，根据输出显示，测得压电变压器的谐振频率为54．8 kHz。实验结果与有限元计算基本一致。
3)疲劳加载除了使多层压电变压器的形变与振动的协调性变差外，还使得整体的振动速率下降，振动幅度变小，升压比降低，约是疲劳前的85％左右 。